Sampling from Arbitrary Functions via PSD Models
Résumé
In many areas of applied statistics and machine learning, generating an arbitrary number of independent and identically distributed (i.i.d.) samples from a given distribution is a key task. When the distribution is known only through evaluations of the density, current methods either scale badly with the dimension or require very involved implementations. Instead, we take a two-step approach by first modeling the probability distribution and then sampling from that model. We use the recently introduced class of positive semi-definite (PSD) models, which have been shown to be efficient for approximating probability densities. We show that these models can approximate a large class of densities concisely using few evaluations, and present a simple algorithm to effectively sample from these models. We also present preliminary empirical results to illustrate our assertions.
Fichier principal
 arxiv.pdf (1.62 Mo)
Télécharger le fichier
arxiv.pdf (1.62 Mo)
Télécharger le fichier
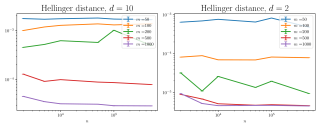 experiment_hellinger_distance_1.pdf (197.82 Ko)
Télécharger le fichier
experiment_hellinger_distance_1.pdf (197.82 Ko)
Télécharger le fichier
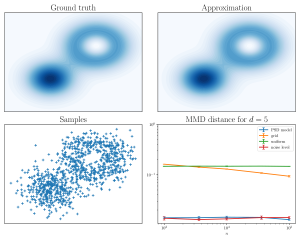 experiment_learning_4.pdf (826.96 Ko)
Télécharger le fichier
experiment_learning_4.pdf (826.96 Ko)
Télécharger le fichier
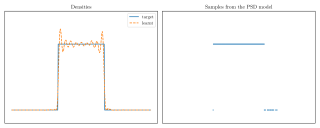 experiment_non_continuous.pdf (76.44 Ko)
Télécharger le fichier
experiment_non_continuous.pdf (76.44 Ko)
Télécharger le fichier
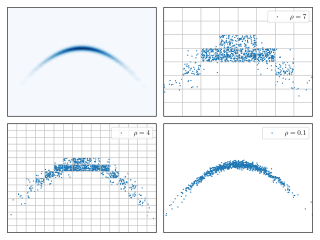 tau_effect_3.pdf (243.99 Ko)
Télécharger le fichier
tau_effect_3.pdf (243.99 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |