Expected Length of the Voronoi Path in a High Dimensional Poisson-Delaunay Triangulation
Longueur moyenne de la marche de Vornoi dans une triangulation de Poisson-Delaunay en dimension $d$
Résumé
Let $X_n$ be a $d$ dimensional
Poisson point process of intensity $n$.
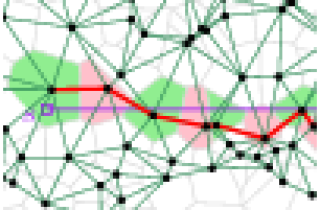
We prove that the expected length of the Voronoi path between two
points at distance 1 in
the Delaunay triangulation associated with $X_n$
is $\sqrt{\frac{2d}{\pi}}+O(d^{-\frac{1}{2}})$ for all $n\in\mathbb{N}$ and $d\rightarrow\infty$.
In any dimension, we provide a precise interval containing the exact
value, in 3D the expected length is between 1.4977 and 1.50007.
Soit $X_n$ un processus ponctuel de Poisson d'intensité $n$ en
dimension $d$.
Nous démontrons que l'espérance de la longueur du chemin de Voronoi
entre l'origine et un point à distance 1 dans la triangulation de
Delaunay de $X_n$ est $\sqrt{\frac{2d}{\pi}}+O(d^{-\frac{1}{2}})$
pour tout $n\in\mathbb{N}$ quand $d\rightarrow\infty$.
Nous donnons des bornes inférieures et supérieures sur la bonne valeur
en toute dimension, en 3D ces bornes sont 1.4977 et 1.50007.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
RR-8947.pdf (861.08 Ko)
Télécharger le fichier
vignette (1).png (14.78 Ko)
Télécharger le fichier
Maple.zip (366.73 Ko)
Télécharger le fichier
vignette.png (18.99 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
Loading...