Growing Least Squares for the Continuous Analysis of Manifolds in Scale-Space
Résumé
We present a novel approach to the multi-scale analysis of point-sampled manifolds of co-dimension 1. It is based on a variant of Moving Least Squares, whereby the evolution of a geometric descriptor at increasing scales is used to locate pertinent locations in scale-space, hence the name "Growing Least Squares". Compared to existing scale-space analysis methods, our approach is the first to provide a continuous solution in space and scale dimensions, without requiring any parametrization, connectivity or uniform sampling. An important implication is that we identify multiple pertinent scales for any point on a manifold, a property that had not yet been demonstrated in the literature. In practice, our approach exhibits an improved robustness to change of input, and is easily implemented in a parallel fashion on the GPU. We compare our method to state-of-the-art scale-space analysis techniques and illustrate its practical relevance in a few application scenarios.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 main.pdf (3.25 Mo)
Télécharger le fichier
main.pdf (3.25 Mo)
Télécharger le fichier
 gls-torus.png (1.22 Mo)
Télécharger le fichier
gls-torus.png (1.22 Mo)
Télécharger le fichier
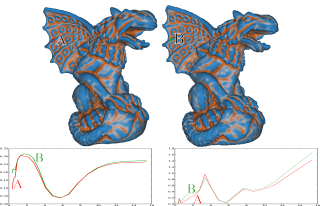 fig-garg.pdf (1.54 Mo)
Télécharger le fichier
fig-garg.pdf (1.54 Mo)
Télécharger le fichier
 pertinentArmadillo.png (691.72 Ko)
Télécharger le fichier
pertinentArmadillo.png (691.72 Ko)
Télécharger le fichier
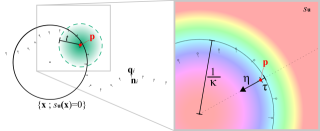 scalarfield_circle.png (337.83 Ko)
Télécharger le fichier
slides-gls.pdf (1.38 Mo)
Télécharger le fichier
scalarfield_circle.png (337.83 Ko)
Télécharger le fichier
slides-gls.pdf (1.38 Mo)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Autre |
|---|