Beating binary powering for polynomial matrices
Résumé
The $N$th power of a polynomial matrix of fixed size and degree can be computed by binary powering as fast as multiplying two polynomials of linear degree in $N$. When Fast Fourier Transform (FFT) is available, the resulting arithmetic complexity is \emph{softly linear} in $N$, i.e. linear in $N$ with extra logarithmic factors. We show that it is possible to beat binary powering, by an algorithm whose complexity is \emph{purely linear} in $N$, even in absence of FFT. The key result making this improvement possible is that the entries of the $N$th power of a polynomial matrix satisfy linear differential equations with polynomial coefficients whose orders and degrees are independent of $N$. Similar algorithms are proposed for two related problems: computing the $N$th term of a C-recursive sequence of polynomials, and modular exponentiation to the power $N$ for bivariate polynomials.
Fichier principal
 BoNeYu23.pdf (598.97 Ko)
Télécharger le fichier
BoNeYu23.pdf (598.97 Ko)
Télécharger le fichier
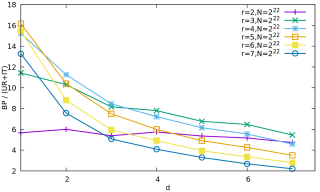 ratio_urit_vs_bp_N22.pdf (8.82 Ko)
Télécharger le fichier
ratio_urit_vs_bp_N22.pdf (8.82 Ko)
Télécharger le fichier
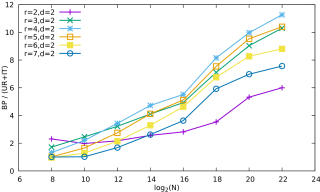 ratio_urit_vs_bp_deg2.pdf (9.39 Ko)
Télécharger le fichier
ratio_urit_vs_bp_deg2.pdf (9.39 Ko)
Télécharger le fichier
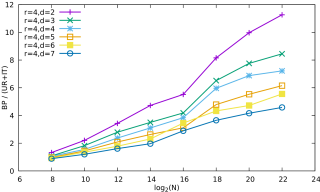 ratio_urit_vs_bp_ord4.pdf (9.4 Ko)
Télécharger le fichier
BoNeYu23.tex (88.72 Ko)
Télécharger le fichier
acmart.cls (114.34 Ko)
Télécharger le fichier
ratio_urit_vs_bp_ord4.pdf (9.4 Ko)
Télécharger le fichier
BoNeYu23.tex (88.72 Ko)
Télécharger le fichier
acmart.cls (114.34 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
| Format | Figure, Image |
|---|

