Floating tangents for approximating spatial curves with G1 piecewise helices
Résumé
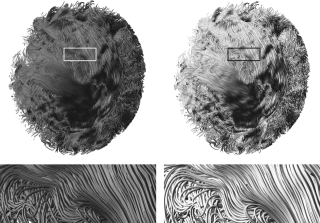
Curves are widely used in computer science to describe real-life objects such as slender deformable structures. Using only 3 parameters per element, piecewise helices offer an interesting and compact way of representing digital curves. In this paper, we present a robust and fast algorithm to approximate Bezier curves with G1 piecewise helices. Our approximation algorithm takes a Bezier spline as input along with an integer N and returns a piecewise helix with N elements that closely approximates the input curve. The key idea of our method is to take N+1 evenly distributed points along the curve, together with their tangents, and interpolate these tangents with helices by slightly relaxing the points. Building on previous work, we generalize the proof for Ghosh's co-helicity condition, which serves us to guarantee the correctness of our algorithm in the general case. Finally, we demonstrate both the efficiency and robustness of our method by successfully applying it to various datasets of increasing complexity, ranging from synthetic curves created by an artist to automatic image-based reconstructions of real data such as hair, heart muscular fibers or magnetic field lines of a star.
Fichier principal
 article.pdf (12.95 Mo)
Télécharger le fichier
article.pdf (12.95 Mo)
Télécharger le fichier
 vignette.png (328.42 Ko)
Télécharger le fichier
vignette.png (328.42 Ko)
Télécharger le fichier
 FloatingTangents.png (3.34 Mo)
Télécharger le fichier
FloatingTangents.png (3.34 Mo)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
Loading...