Articulated Shape Matching Using Laplacian Eigenfunctions and Unsupervised Point Registration
Résumé
Matching articulated shapes represented by voxelsets reduces to maximal sub-graph isomorphism when each set is described by a weighted graph. Spectral graph theory can be used to isometrically map these graphs onto lower dimensional spaces and match shapes by aligning their embeddings in virtue of their invariance to change of pose. Classical graph isomorphism schemes relying on the ordering of the eigenvalues to align Laplacian eigenvectors fail when handling large data-sets or noisy data. We derive a new formulation equivalent to finding the best alignment between two congruentK-dimensional sets of points, where the dimensionK of the embedding space results from the selection of the best subset of eigenfunctions of the Laplacian operator. This set is detected by matching the signatures of those eigenfunctions expressed as histograms, and provides a smart initialization for the alignment problem with a considerable impact on the overall performance. Dense matching then reduces to point registration of embeddings under orthogonal transformations; a task we cast into the framework of unsupervised clustering and solve using the EM algorithm. Maximal subset matching of non identical shapes is handled by defining an appropriate outlier class. Experimental results on challenging examples show how the algorithm naturally treats changes of topology, shape variations and different sampling densities.
Fichier principal
 mateus_MHKCB08_cvpr2008.pdf (793.74 Ko)
Télécharger le fichier
mateus_MHKCB08_cvpr2008.pdf (793.74 Ko)
Télécharger le fichier
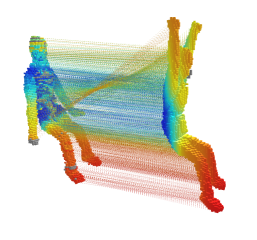 mannequin_match_pose3_pose4.png (472.68 Ko)
Télécharger le fichier
CVPR2008-final.mov (8.19 Mo)
Télécharger le fichier
mannequin_match_pose3_pose4.png (472.68 Ko)
Télécharger le fichier
CVPR2008-final.mov (8.19 Mo)
Télécharger le fichier
 mannequin_pose1.png (202.22 Ko)
Télécharger le fichier
mannequin_pose1.png (202.22 Ko)
Télécharger le fichier
 mars_pose70.png (118.76 Ko)
Télécharger le fichier
mars_pose70.png (118.76 Ko)
Télécharger le fichier
 match_k26_expo_d20_Mannmann-sim.png (260.44 Ko)
Télécharger le fichier
match_k26_expo_d20_Mannmann-sim.png (260.44 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Autre |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
Loading...