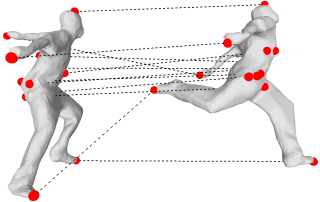
We address the problem of matching two 3D shapes by representing them using the eigenvalues and eigenvectors of the discrete diffusion operator. This provides a representation framework useful for both scale-space shape descriptors and shape comparisons. We formally introduce a canonical diffusion embedding based on the combinatorial Laplacian; we reveal some interesting properties and we propose a unit hypersphere normalization of this embedding. We also propose a practical algorithm that seeks the largest set of mutually consistent point-to-point matches between two shapes based on isometric consistency between the two embeddings. We illustrate our method with several examples of matching shapes at various scales.