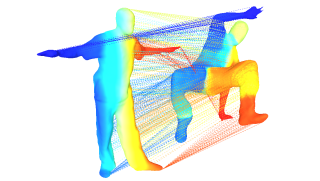
In this paper we propose an inexact spectral matching algorithm that embeds large graphs on a low-dimensional isometric space spanned by a set of eigenvectors of the graph Laplacian. Given two sets of eigenvectors that correspond to the smallest non-null eigenvalues of the Laplacian matrices of two graphs, we project each graph onto its eigenenvectors. We estimate the histograms of these one-dimensional graph projections (eigenvector histograms) and we show that these histograms are well suited for selecting a subset of significant eigenvectors, for ordering them, for solving the sign-ambiguity of eigenvector computation, and for aligning two embeddings. This results in an inexact graph matching solution that can be improved using a rigid point registration algorithm. We apply the proposed methodology to match surfaces represented by meshes.