Accurate Detection of Symmetries in 3D Shapes
Résumé
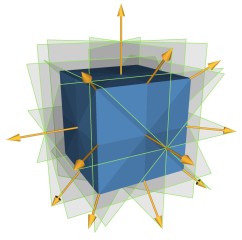
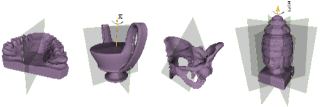
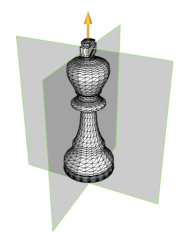
We propose an automatic method for finding symmetries of 3D shapes, i.e. isometric transforms which leave a shape globally unchanged. These symmetries are deterministically found through the use of an intermediate quantity: the generalized even moments. By examining their extrema and spherical harmonic coefficients we recover the parameters of the symmetries of the shape. The computation for large composite models is made efficient by using this information in an incremental algorithm capable of recovering the symmetries of a whole shape using the symmetries of its sub-parts. Applications of this work range from coherent re-meshing of geometry with respect to the symmetries of a shape, to geometric compression, intelligent mesh editing and automatic instantiation.
Fichier principal
SymmetrieDetectionTOG.pdf (728.41 Ko)
Télécharger le fichier
cube.jpg (172.84 Ko)
Télécharger le fichier
PowerPlantEx.png (355.14 Ko)
Télécharger le fichier
ScannedModelsExample.png (47.99 Ko)
Télécharger le fichier
Teeth.jpg (67.82 Ko)
Télécharger le fichier
gradient1.jpg (64.1 Ko)
Télécharger le fichier
king.jpg (96.03 Ko)
Télécharger le fichier
pipeExample.png (26.69 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
Loading...