Markov and semi-Markov switching linear mixed models for identifying forest tree growth components.
Résumé
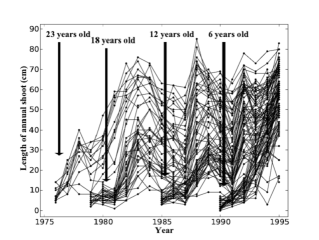
Observed tree growth is the result of three components: (i) an endogenous component which is assumed to be structured as a succession of roughly stationary phases separated by marked change points asynchronous between individuals, (ii) a time-varying environmental component which is assumed to take the form of local fluctuations synchronous between individuals, (iii) an individual component which corresponds to the local environmental of each tree. In order to identify and to characterize these three omponents, we propose to use semi-Markov switching linear mixed models, i.e. models that combine linear mixed models in a semi-markovian manner. The underlying semi-Markov chain represents the succession of growth phases (endogenous component) while the linear mixed models attached to each state of the underlying semi-Markov chain represent in the corresponding growth phase both the influence of time-varying environmental covariates (environmental component) as fixed effects and inter-individual heterogeneity (individual component) as random effects. In this paper, we address the estimation of Markov and semi-Markov switching linear mixed models in a general framework. We propose a MCEM-like algorithm whose iterations decompose into three steps (sampling of state sequences given random effects, prediction of random effects given the state sequence and maximization). The proposed statistical modeling approach is illustrated by the analysis of successive annual shoots along Corsican pine trunks influenced by climatic covariates.
Fichier principal
 RR-6618.pdf (595 Ko)
Télécharger le fichier
RR-6618.pdf (595 Ko)
Télécharger le fichier
 annualshootlenghts.png (226.4 Ko)
Télécharger le fichier
annualshootlenghts.png (226.4 Ko)
Télécharger le fichier
| Origine | Accord explicite pour ce dépôt |
|---|
| Format | Figure, Image |
|---|
Loading...