Covering families of triangles
Résumé
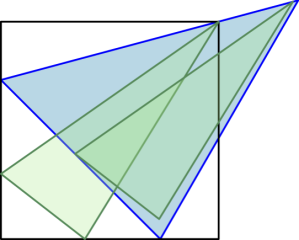
A cover for a family F of sets in the plane is a set into which every set in F can be isometrically moved. We are interested in the convex cover of smallest area for a given family of triangles. Park and Cheong conjectured that any family of triangles of bounded diameter has a smallest convex cover that is itself a triangle. The conjecture is equivalent to the claim that for every convex set X there is a triangle Z whose area is not larger than the area of X , such that Z covers the family of triangles contained in X. We prove this claim for the case where a diameter of X lies on its boundary. We also give a complete characterization of the smallest convex cover for the family of triangles contained in a half-disk, and for the family of triangles contained in a square. In both cases, this cover is a triangle.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
hal.pdf (1.09 Mo)
Télécharger le fichier
vignette.png (43.13 Ko)
Télécharger le fichier
computations.mw.gz (76.78 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
