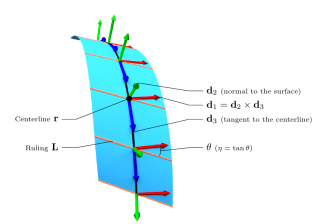
We propose a robust and efficient numerical model to compute stable equilibrium configurations of clamped elastic ribbons featuring arbitrarily curved natural shapes. Our spatial discretization scheme relies on elements characterized by a linear normal curvature and a quadratic geodesic torsion with respect to arc length. Such a high-order discretization allows for a great diversity of kine-matic representations, while guaranteeing the surface of the ribbon to remain perfectly inextensible. Stable equilibria are calculated by minimizing the sum of the gravitational and elastic energies of the ribbon, under a developability constraint. Our algorithm compares favorably to standard shooting and collocation methods, as well as to experiments. It furthermore shows significant differences in behavior compared to numerical models for thin elastic rods, while yielding a substantial speed-up compared to a more general thin elastic shell simula-tor. These results confirm the benefit of designing a special numerical model dedicated to ribbons..