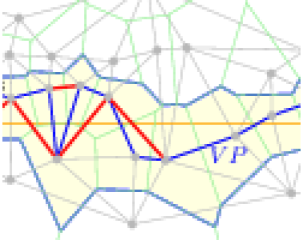
Let $X_n$ be a planar Poisson point process of intensity $n$. We give a new proof that the expected length of the Voronoi path between $(0,0)$ and $(1,0)$ in the Delaunay triangulation associated with $X_n$ is $\tfrac{4}{\pi}\simeq 1.27$ when $n$ goes to infinity; and we also prove that the variance of this length is $\Theta(1/\sqrt{n})$. We investigate the length of possible shortcuts in this path, and define a shortened Voronoi path whose expected length can be expressed as an integral that is numerically evaluated to $\simeq 1.16$. The shortened Voronoi path has the property to be {\em locally defined}; and is shorter than the previously known locally defined paths in Delaunay triangulation such as the upper path whose expected length is $35/3\pi^2\simeq 1.18$.