Anisotropic Delaunay Mesh Generation
Résumé
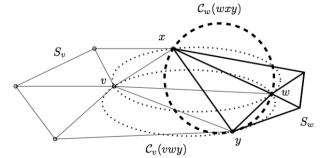
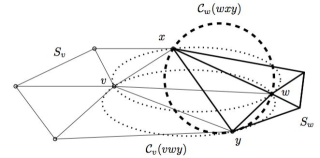
Anisotropic meshes are triangulations of a given domain in the plane or in higher dimensions, with elements elongated along prescribed directions. Anisotropic trian-gulations are known to be well suited for interpolation of functions or solving PDEs. Assuming that the anisotropic shape requirements for mesh elements are given through a metric field varying over the domain, we propose a new approach to anisotropic mesh generation, relying on the notion of anisotropic Delaunay meshes. An anisotropic De-launay mesh is defined as a mesh in which the star of each vertex v consists of simplices that are Delaunay for the metric associated to vertex v. This definition works in any dimension and allows to define a simple refinement algorithm. The algorithm takes as input a domain and a metric field and provides, after completion, an anisotropic mesh whose elements are sized and shaped according to the metric field.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 main-final.pdf (611.42 Ko)
Télécharger le fichier
main-final.pdf (611.42 Ko)
Télécharger le fichier
 vignette.png (44.8 Ko)
Télécharger le fichier
vignette.png (44.8 Ko)
Télécharger le fichier
 vignette.jpg (26.86 Ko)
Télécharger le fichier
vignette.jpg (26.86 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |