A Probabilistic Approach to Reducing Algebraic Complexity of Delaunay Triangulations
Résumé
We propose algorithms to compute the Delaunay triangulation of a point set L using only (squared) distance comparisons (i.e., predicates of degree 2). Our approach is based on the witness complex, a weak form of the Delaunay complex introduced by Carlsson and de Silva. We give conditions that ensure that the witness complex and the Delaunay triangulation coincide and we introduce a new perturbation scheme to compute a perturbed set L′ close to L such that the Delaunay triangulation and the witness complex coincide. Our perturbation algorithm is a geometric application of the Moser-Tardos constructive proof of the Lovász local lemma.
Fichier principal
 esa.pdf (316.36 Ko)
Télécharger le fichier
esa.pdf (316.36 Ko)
Télécharger le fichier
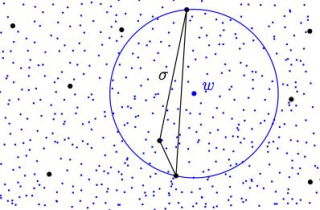 witness-complex.jpg (24.5 Ko)
Télécharger le fichier
witness-complex.jpg (24.5 Ko)
Télécharger le fichier
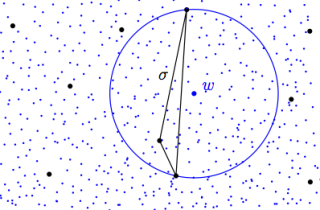 witness-complex.png (35.65 Ko)
Télécharger le fichier
witness-complex.png (35.65 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
Loading...