Piecewise polynomial monotonic interpolation of 2D gridded data
Résumé
A method for interpolating monotone increasing 2D scalar data with a monotone piecewise cubic C$^1$-continuous surface is presented. Monotonicity is a sufficient condition for a function to be free of critical points inside its domain. The standard axial monotonicity for tensor-product surfaces is however too restrictive. We therefore introduce a more relaxed monotonicity constraint. We derive sufficient conditions on the partial derivatives of the interpolating function to ensure its monotonicity. We then develop two algorithms to effectively construct a monotone C$^1$ surface composed of cubic triangular Bézier surfaces interpolating a monotone gridded data set. Our method enables to interpolate given topological data such as minima, maxima and saddle points at the corners of a rectangular domain without adding spurious extrema inside the function domain. Numerical examples are given to illustrate the performance of the algorithm.
Fichier principal
 AllemandGiorgisSpringerBookChapterAuthorPreprint.pdf (3.67 Mo)
Télécharger le fichier
AllemandGiorgisSpringerBookChapterAuthorPreprint.pdf (3.67 Mo)
Télécharger le fichier
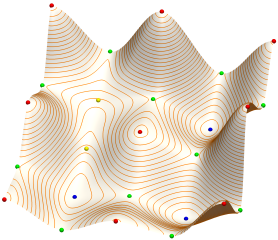 TopoPreservImage.png (1.76 Mo)
Télécharger le fichier
TopoPreservImage.png (1.76 Mo)
Télécharger le fichier
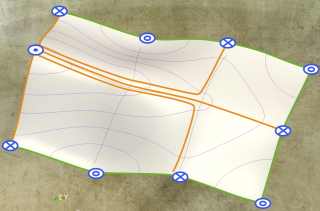 FunctionReconstruction.png (1.44 Mo)
Télécharger le fichier
FunctionReconstruction.png (1.44 Mo)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
Loading...