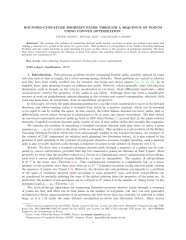
Bounded-Curvature Shortest Paths through a Sequence of Points using Convex Optimization
Résumé
We consider the problem of computing shortest paths having curvature at most one almost everywhere and visiting a sequence of $n$ points in the plane in a given order. This problem is a sub-problem of the Dubins Traveling Salesman Problem and also arises naturally in path planning for point car-like robots in the presence of polygonal obstacles. We show that when consecutive waypoints are distance at least four apart, this question reduces to a family of convex optimization problems over polyhedra in $\mathbb{R}^n$.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
viapoints_final.pdf (330.92 Ko)
Télécharger le fichier
2013 Bounded-Curvature Shortest Paths.png (48.39 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
Loading...