Noise-Adaptive Shape Reconstruction from Raw Point Sets
Résumé
We propose a noise-adaptive shape reconstruction method specialized to smooth, closed shapes. Our algorithm takes as input a defect-laden point set with variable noise and outliers, and comprises three main steps. First, we compute a novel noise-adaptive distance function to the inferred shape, which relies on the assumption that the inferred shape is a smooth submanifold of known dimension. Second, we estimate the sign and confidence of the function at a set of seed points, through minimizing a quadratic energy expressed on the edges of a uniform random graph. Third, we compute a signed implicit function through a random walker approach with soft constraints chosen as the most confident seed points computed in previous step.
Domaines
Géométrie algébrique [math.AG]
Fichier principal
 reconstruction2.pdf (399.81 Ko)
Télécharger le fichier
reconstruction2.pdf (399.81 Ko)
Télécharger le fichier
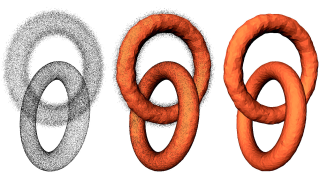 reconstruction_tori.jpg (570.83 Ko)
Télécharger le fichier
reconstruction_tori.jpg (570.83 Ko)
Télécharger le fichier
 noiseadaptive.png (56.19 Ko)
Télécharger le fichier
noiseadaptive.png (56.19 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
Loading...