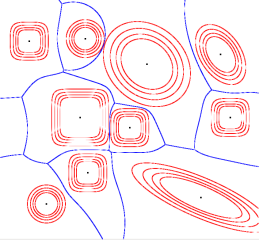
We design and implement an efficient and certified algorithm for the computation of Voronoi Diagrams (VD's) constrained to a given domain. Our framework is general and applicable to any VD-type where the distance field is given explicitly or implicitly by a polynomial, notably the anisotropic VD or VD's of non-punctual sites. We use the Bernstein form of polynomials and DeCasteljau's algorithm to subdivide the initial domain and isolate bisector, or domains that contain a Voronoi vertex. The efficiency of our algorithm is due to a filtering process, based on bounding the field over the subdivided domains. This allows to exclude functions (thus sites) that do not contribute locally to the lower envelope of the lifted diagram. The output is a polygonal description of each Voronoi cell, within any user-defined precision, isotopic to the exact VD. Correctness of the result is implied by the certified approximations of bisector branches, which are computed by existing methods for handling algebraic curves. First experiments with our C++ implementation, based on double precision arithmetic, demonstrate the adaptability of the algorithm.