The Voronoi diagram of three lines
Résumé
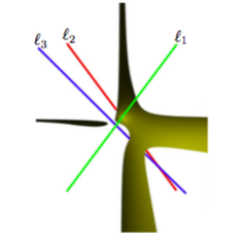
We give a complete description of the Voronoi diagram, in $\R^3$, of three lines in general position, that is, that are pairwise skew and not all parallel to a common plane. In particular, we show that the topology of the Voronoi diagram is invariant for three such lines. The trisector consists of four unbounded branches of either a non-singular quartic or of a non-singular cubic and a line that do not intersect in real space. Each cell of dimension two consists of two connected components on a hyperbolic paraboloid that are bounded, respectively, by three and one of the branches of the trisector. We introduce a proof technique, which relies heavily upon modern tools of computer algebra, and is of interest in its own right. This characterization yields some fundamental properties of the Voronoi diagram of three lines. In particular, we present linear semi-algebraic tests for separating the two connected components of each two-dimensional Voronoi cell and for separating the four connected components of the trisector. This enables us to answer queries of the form, given a point, determine in which connected component of which cell it lies. We also show that the arcs of the trisector are monotonic in some direction. These properties imply that points on the trisector of three lines can be sorted along each branch using only linear semi-algebraic tests.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 Voronoi3lines_revised.pdf (662.01 Ko)
Télécharger le fichier
Voronoi3lines_revised.pdf (662.01 Ko)
Télécharger le fichier
 2009 Voronoi diagram of three lines.png (35.47 Ko)
Télécharger le fichier
2009 Voronoi diagram of three lines.png (35.47 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
Loading...