Compatible Embedding for 2D Shape Animation
Abstract
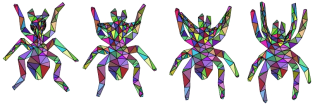
We present new algorithms for the compatible embedding of 2D shapes. Such embeddings offer a convenient way to interpolate shapes having complex, detailed features. Compared to existing techniques, our approach requires less user input, is faster, more robust, and simpler to implement, making it ideal for interactive use in practical applications. Our new approach consists of three parts. First, our boundary matching algorithm locates salient features using the perceptually-motivated principles of scale-space and uses these as automatic correspondences to guide an elastic curve matching algorithm. Second, we simplify boundaries while maintaining their parametric correspondence and the embedding of the original shapes. Finally, we extend the mapping to shapes' interiors via a new compatible triangulation algorithm. The combination of our algorithms allows us to demonstrate 2D shape interpolation with instant feedback. The proposed algorithms exhibit a combination of simplicity, speed, and accuracy that has not been achieved in previous work.
Domains
Graphics [cs.GR]
Fichier principal
 CompatibleEmbedding-OLMTRE-2008-001.pdf (2.06 Mo)
Télécharger le fichier
CompatibleEmbedding-OLMTRE-2008-001.pdf (2.06 Mo)
Télécharger le fichier
 arachno0Match.jpg (52.65 Ko)
Télécharger le fichier
arachno0Match.jpg (52.65 Ko)
Télécharger le fichier
 arachno1Simp.jpg (41.93 Ko)
Télécharger le fichier
arachno1Simp.jpg (41.93 Ko)
Télécharger le fichier
 arachno2Mesh.jpg (138.27 Ko)
Télécharger le fichier
arachno2Mesh.jpg (138.27 Ko)
Télécharger le fichier
| Origin | Files produced by the author(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
Loading...