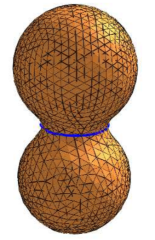
Constrictions on a surface are defined as simple closed curves whose length is locally minimal. In particular, constrictions are periodic geodesics. We use constrictions in order to segment objects. In [Hetroy and Attali, VisSym 2003], we proposed an approach based on progressive surface simplification and local geodesic computation. The drawback of this approach is that constrictions are approximated by closed piecewise geodesics which are not necessarily periodic geodesics. In this paper, we compute constrictions starting from the closed piecewise geodesics previously computed and moving them on the surface. We compare the location of the initial closed piecewise geodesics to the location of the constrictions. Finally, we define and compute different types of constrictions on a surface.