Six Methods for Transforming Layered Hypergraphs to Apply Layered Graph Layout Algorithms
Résumé
Hypergraphs are a generalization of graphs in which edges (hyperedges) can connect more than two vertices-as opposed to ordinary graphs where edges involve only two vertices. Hypergraphs are a fairly common data structure but there is little consensus on how to visualize them. To optimize a hypergraph drawing for readability, we need a layout algorithm. Common graph layout algorithms only consider ordinary graphs and do not take hyperedges into account. We focus on layered hypergraphs, a particular class of hypergraphs that, like layered graphs, assigns every vertex to a layer, and the vertices in a layer are drawn aligned on a linear axis with the axes arranged in parallel. In this paper, we propose a general method to apply layered graph layout algorithms to layered hypergraphs. We introduce six different transformations for layered hypergraphs. The choice of transformation affects the subsequent graph layout algorithm in terms of computational performance and readability of the results. Thus, we perform a comparative evaluation of these transformations in terms of number of crossings, edge length, and impact on performance. We also provide two case studies showing how our transformations can be applied to real-life use cases. A copy of this paper with all appendices and supplemental material is available at osf.io/grvwu.
Domaines
Interface homme-machine [cs.HC]
Fichier principal
 v41i3pp259-270.pdf (1.96 Mo)
Télécharger le fichier
v41i3pp259-270.pdf (1.96 Mo)
Télécharger le fichier
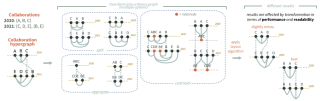 barycentric.png (124.73 Ko)
Télécharger le fichier
barycentric.png (124.73 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Licence |


