Flexible G1 Interpolation of Quad Meshes
Résumé
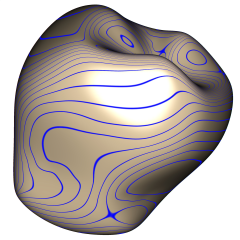
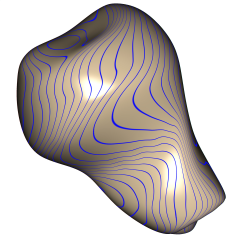
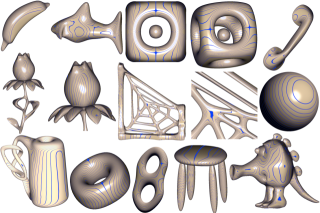
Transforming an arbitrary mesh into a smooth G1 surface has been the subject of intensive research works. To get a visual pleasing shape without any imperfection even in the presence of extraordinary mesh vertices is still a challenging problem in particular when interpolation of the mesh vertices is required. We present a new local method, which produces visually smooth shapes while solving the interpolation problem. It consists of combining low degree biquartic Bézier patches with minimum number of pieces per mesh face, assembled together with G1-continuity. All surface control points are given explicitly. The construction is local and free of zero-twists. We further show that within this economical class of surfaces it is however possible to derive a sufficient number of meaningful degrees of freedom so that standard optimization techniques result in high quality surfaces.
Fichier principal
 FlexibleG1QuadLowRes.pdf (780.84 Ko)
Télécharger le fichier
FlexibleG1QuadLowRes.pdf (780.84 Ko)
Télécharger le fichier
 AllGumbys.png (3.03 Mo)
Télécharger le fichier
AllGumbys.png (3.03 Mo)
Télécharger le fichier
 AppleAndVaseLarge_25.png (2.52 Mo)
Télécharger le fichier
AppleAndVaseLarge_25.png (2.52 Mo)
Télécharger le fichier
 AppleQuartic.jpg (775.39 Ko)
Télécharger le fichier
AppleQuartic.jpg (775.39 Ko)
Télécharger le fichier
 CubeNousEq1_5.png (2.68 Mo)
Télécharger le fichier
CubeNousEq1_5.png (2.68 Mo)
Télécharger le fichier
 CubeNousSphere.png (3.33 Mo)
Télécharger le fichier
CubeNousSphere.png (3.33 Mo)
Télécharger le fichier
 DuckLarge.png (2.71 Mo)
Télécharger le fichier
DuckLarge.png (2.71 Mo)
Télécharger le fichier
 PearQuartic.jpg (702.98 Ko)
Télécharger le fichier
PearQuartic.jpg (702.98 Ko)
Télécharger le fichier
 Surfaces-Opt.png (1.64 Mo)
Télécharger le fichier
Surfaces-Opt.png (1.64 Mo)
Télécharger le fichier
 ToreCarreQuartic.jpg (875.93 Ko)
Télécharger le fichier
ToreCarreQuartic.jpg (875.93 Ko)
Télécharger le fichier
 ZoomComparaisonCatmull.png (2.06 Mo)
Télécharger le fichier
ZoomComparaisonCatmull.png (2.06 Mo)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
Loading...