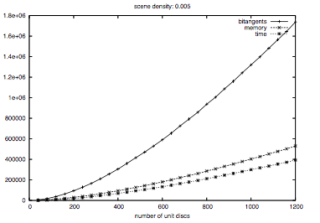
We study the expected size of the 2D visibility complex of randomly distributed objects in the plane. We prove that the asymptotic expected number of free bitangents (which correspond to 0-faces of the visibility complex) among unit discs (or polygons of bounded aspect ratio and similar size) is linear and exhibit bounds in terms of the density of the objects. We also make an experimental assessment of the size of the visibility complex for disjoint random unit discs. We provide experimental estimates of the onset of the linear behavior and of the asymptotic slope and $y$-intercept of the number of free bitangents in terms of the density of discs. Finally, we analyze the quality of our estimates in terms of the density of discs.